https://docs.google.com/presentation/d/1OwOpVgblSo0GvY1Z3XK2TvGP9QgLHDo8/edit?usp=drivesdk&ouid=105830913094188274202&rtpof=true&sd=true
divendres, 21 d’octubre del 2022
divendres, 14 de gener del 2022
2021-desembre-eixample bcn
Si vols veure la presentació completa, clica el següent enllaç
https://drive.google.com/file/d/1S4VStQwKijWhSUEak-e75WUvc3vZcPSQ/view?usp=drivesdk
Fust tors (geom) 20210811_01
Si vols veure la presentació completa, clica el següent enllaç
https://drive.google.com/file/d/1SGoq3Nc3JIFg3tD0NrWgVtF1Ut7mUBRK/view?usp=drivesdk
2021-juliol-escala de Jacob
https://drive.google.com/file/d/1ebVtwtxWz7UiSpdnSgjgp1R061BzWgtH/view?usp=drivesdk
2021-abril-Laberint al Montsec de Rubies (estudi)
Si vols veure la presentació completa, clica el següent enllaç
https://drive.google.com/file/d/1S7xmxU59BgXlljdbUo5v8ijKPvuj3hq9/view?usp=drivesdk
2021-maig-arbre ocell sense fils
Si vols veure la presentació completa, clica el següent enllaç
https://drive.google.com/file/d/1SDXwDX1MV-AxoFmciXWlf5ja1sAAh3yY/view?usp=drivesdk
dijous, 22 d’octubre del 2020
2020 juny: COLLAR 8p5040c
OBRA FINALITZADA
Dades:
Títol obra: COLLAR 8p5040c
Dimensions: 21 cm x 21 cm x 3 cm
Material: Plàstic ABS imprès.
Descripció:
És un collar de vocació escultòrica, format per vuit peces idèntiques d'ABS, fetes amb impressora 3D. Cada peça té a cada un dels seus dos extrems un encaix que permet el muntatge lineal unidireccional (total o parcial) amb la resta de peces, amb disposició anular plana (en principi).
Per parelles, la secció central (regular) de les peces és o circular (0), o triangular (3 costats), o quadrangular (4 costats) o pentagonal (5 costats).
L'elecció de aquests nombres sencers (3, 4 i 5) és un homenatge a la corda de dotze nusos pre-pitagòrica (3 ; 4 ; 5) que feien servir de manera comuna els antics egipcis.
La duplicitat de seccions centrals d'aquestes peces (2 de "0"; 2 de "3"; 2 de "4" i 2 de "5") només té la funció d'incrementar la combinatòria del conjunt del collar.
El conjunt té una morfologia tubular corba, i d'aspecte lleugerament bulbós, amb grups de perforacions cilíndriques paral·leles entre si, però disposades obliquament envers cada peça.
L'ordre en què les anem col·locant es correspon a un sistema combinatori circular o tancat del tipus permutació sense repetició.
Tenim 8 elements diferents combinats de 8 en 8.
Donat que és un sistema tancat o circular, la quantitat de combinacions diferents total és factorial de 8 menys 1. Factorial de 7 és 5040.
Això ens dóna 5040 combinacions diferents.
Collar format per 8 peces corbes amb disposició anular plana.
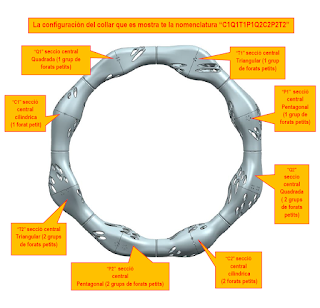
‘--- 2 peces diferents, de seccio central cilíndrica (0). Las batejem com “C1” i “C2”.
“C1” te nomes un forat petit en un dels costats de la curvatura principal de la peça, i “C2” en te dos.
‘--- 2 peces diferents, de seccio central triangular (3). Las batejem com “T1” i “T2”.
“T1” te un grup de 3 forats petits en un dels costats de la curvatura principal de la peça, i “T2” en te dos.
‘--- 2 peces diferents, de seccio central quadrada (4). Las batejem com “Q1” i “Q2”.
“Q1” te un grup de 4 forats petits en un dels costats de la curvatura principal de la peça, i “Q2” en te dos.
‘--- 2 peces diferents, de seccio central pentagonal (5). Las batejem com “P1” i “P2”.
“P1” te un grup de 5 forats petits en un dels costats de la curvatura principal de la peça, i “P2” en te dos.
En cada una d’aquestes parelles, l’angle de torsió de la seccio central respecte al pla de curvatura principal del collar es diferent.
Pero la duplicitat de seccions centrals d’aquestes peces (2 de “0”; 2 de “3”; 2 de “4” i 2 de “5”) només te la funció de incrementar la combinatoria del conjunt del collar.
Com a convenció, La peça “C1” es pot definir com l’inici de la sequencia.
Esclar que pel fet de ser una squencia tancada no existeix un inici real.
Disposem aquesta peça “C1” amb el el forat lateral visible, i anem conectan la resta de peces en sentit dextrogir (sentit de gir de les busques del relotge). Aixó farà que els grups de forats petits estigui sempre visible.
El ordre en que les anem colocan es correspon a un sistema combinatori circular o tancat del tipus permutació sense repetició. Tenim 8 elements diferents combinants de 8 en 8.
Donat que es un sistema tancat o circular, la quantitat de combinacions diferentes total es factorial de 8 mens 1. Factorial de 7 es 5040.
Aixo ens dona 5040 combinacions diferentes.
Aquí están totes:
1 C1 C2 T1 T2 Q1 Q2 P1 P2
2 C1 C2 T1 T2 Q1 Q2 P2 P1
3 C1 C2 T1 T2 Q1 P1 Q2 P2
4 C1 C2 T1 T2 Q1 P1 P2 Q2
5 C1 C2 T1 T2 Q1 P2 Q2 P1
6 C1 C2 T1 T2 Q1 P2 P1 Q2
7 C1 C2 T1 T2 Q2 Q1 P1 P2
8 C1 C2 T1 T2 Q2 Q1 P2 P1
.../...
5007 C1 P2 P1 Q1 T2 T1 C2 Q2
5008 C1 P2 P1 Q1 T2 T1 Q2 C2
5009 C1 P2 P1 Q1 T2 Q2 C2 T1
5010 C1 P2 P1 Q1 T2 Q2 T1 C2
5011 C1 P2 P1 Q1 Q2 C2 T1 T2
5012 C1 P2 P1 Q1 Q2 C2 T2 T1
5013 C1 P2 P1 Q1 Q2 T1 C2 T2
5014 C1 P2 P1 Q1 Q2 T1 T2 C2
5015 C1 P2 P1 Q1 Q2 T2 C2 T1
5016 C1 P2 P1 Q1 Q2 T2 T1 C2
5017 C1 P2 P1 Q2 C2 T1 T2 Q1
5018 C1 P2 P1 Q2 C2 T1 Q1 T2
5019 C1 P2 P1 Q2 C2 T2 T1 Q1
5020 C1 P2 P1 Q2 C2 T2 Q1 T1
5021 C1 P2 P1 Q2 C2 Q1 T1 T2
5022 C1 P2 P1 Q2 C2 Q1 T2 T1
5023 C1 P2 P1 Q2 T1 C2 T2 Q1
5024 C1 P2 P1 Q2 T1 C2 Q1 T2
5025 C1 P2 P1 Q2 T1 T2 C2 Q1
5026 C1 P2 P1 Q2 T1 T2 Q1 C2
5027 C1 P2 P1 Q2 T1 Q1 C2 T2
5028 C1 P2 P1 Q2 T1 Q1 T2 C2
5029 C1 P2 P1 Q2 T2 C2 T1 Q1
5030 C1 P2 P1 Q2 T2 C2 Q1 T1
5031 C1 P2 P1 Q2 T2 T1 C2 Q1
5032 C1 P2 P1 Q2 T2 T1 Q1 C2
5033 C1 P2 P1 Q2 T2 Q1 C2 T1
5034 C1 P2 P1 Q2 T2 Q1 T1 C2
5035 C1 P2 P1 Q2 Q1 C2 T1 T2
5036 C1 P2 P1 Q2 Q1 C2 T2 T1
5037 C1 P2 P1 Q2 Q1 T1 C2 T2
5038 C1 P2 P1 Q2 Q1 T1 T2 C2
5039 C1 P2 P1 Q2 Q1 T2 C2 T1
5040 C1 P2 P1 Q2 Q1 T2 T1 C2. Fi de la llista.
Subscriure's a:
Missatges (Atom)